User Manual

Chapitre 3 : Application Graphe & Table 117
• Valeur minimale dans la plage indiquée sur la fenêtre graphique .......................... Analysis - G-Solve - f Min
• Valeur maximale dans la plage indiquée sur la fenêtre graphique ........................ Analysis - G-Solve -
f Max
• Intersection avec l’axe des
y .......................................................................... Analysis - G-Solve - y-Intercept
• Point d’intersection de deux courbes ........................................................... Analysis - G-Solve - Intersection
• Valeur d’intégration pour une plage particulière ......................................... Analysis - G-Solve - Integral - ∫
dx
• Valeur d’intégration entre deux ou plusieurs racines de courbes ............ Analysis - G-Solve - Integral - Root
• Valeur d’intégration entre deux ou plusieurs intersections
de deux courbes ...................................................................... Analysis - G-Solve - Integral - Intersection
• Point d’inflexion .................................................................................................Analysis - G-Solve - Inflection
• Distance entre deux points ............................................................................... Analysis - G-Solve - Distance
• Volume d’un solide de révolution ..................................................................... Analysis - G-Solve - π
∫ f(x)
2
dx
Conseil :
Voir « Types de graphes et fonctions exécutables » (page 314) pour le détail sur les types de courbes et les
fonctions G-Solve qui peuvent être exécutés.
Emploi des commandes du menu G-Solve
Lorsque plusieurs solutions sont obtenues par une commande G-Solve, une seule solution s’affiche à la fois.
Par exemple, exécuter [Analysis] - [G-Solve] - [Root] pour une fonction cubique qui a deux racines, affichera
une seule racine à la fois. En pareil cas, utilisez les touches gauche ou droite du pavé directionnel (ou tapez
sur la flèche gauche ou droite de la commande graphique) pour parcourir les différentes solutions.
u Obtenir la racine d’une fonction
1. Sur la fenêtre de l’éditeur de graphes, saisissez et sauvegardez une fonction, puis tapez sur $ pour la
représenter graphiquement.
• À cet endroit, saisissez
y = x(x + 2)(x – 2) dans la ligne y1.
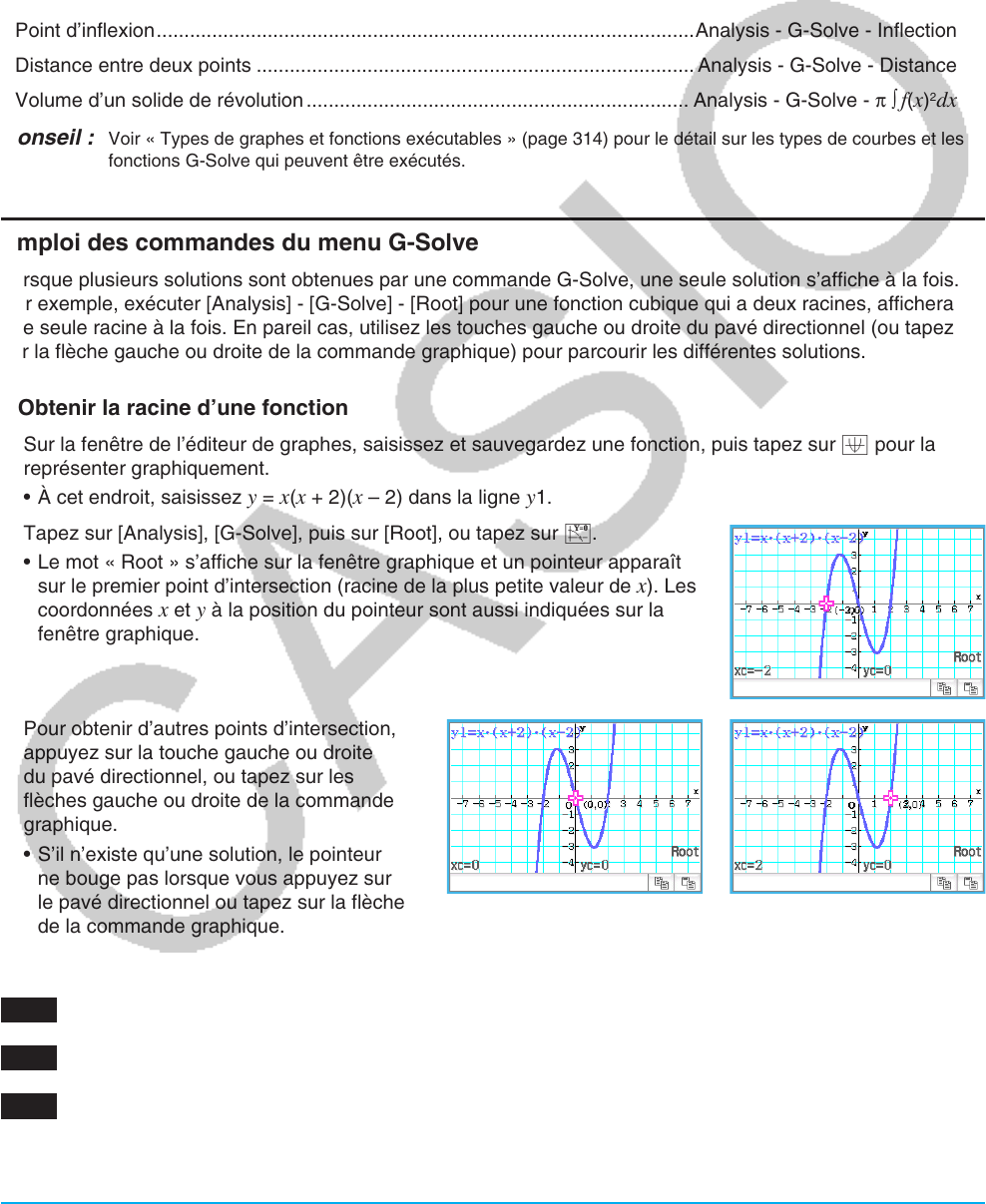
2. Tapez sur [Analysis], [G-Solve], puis sur [Root], ou tapez sur Y.
• Le mot « Root » s’affiche sur la fenêtre graphique et un pointeur apparaît
sur le premier point d’intersection (racine de la plus petite valeur de
x). Les
coordonnées x et y à la position du pointeur sont aussi indiquées sur la
fenêtre graphique.
3. Pour obtenir d’autres points d’intersection,
appuyez sur la touche gauche ou droite
du pavé directionnel, ou tapez sur les
flèches gauche ou droite de la commande
graphique.
• S’il n’existe qu’une solution, le pointeur
ne bouge pas lorsque vous appuyez sur
le pavé directionnel ou tapez sur la flèche
de la commande graphique.
Les exemples suivants concernent les autres commandes G-Solve.
0307 Obtenir les coordonnées d’un point d’intersection de deux courbes
y = x + 1 et y = x
2
0308 Déterminer les coordonnées d’un point particulier d’une courbe
0309 Représenter graphiquement la fonction
y = x(x + 2)(x – 2) et obtenir son intégrale définie dans le
domaine 1 s x s 2